Expected value of a maxlogLreg model.

This function takes a maxlogL model and computes the expected value using the estimated parameters. The expected value is computed using the following expression

$$\hat{E[g(X)]} = \int_{-\infty}^{\infty} x f(x|\hat{\theta}) dx,$$

where \(f(x|\hat{\theta})\) is a probability density function using the estimated parameters.

Usage

expected_value.maxlogL(object, g = identity, routine, ...)

Arguments

object

an object of maxlogL class obtained by fitting a model with maxlogLreg.

g

a given function \(g(x)\).

routine

a character specifying the integration routine. integrate and gauss_quad are available for continuous distributions, and summate for discrete ones. Custom routines can be defined but they must be compatible with the integration API.

...

further arguments for the integration routine.

Value

the expected value of the fitted model corresponding to the distribution specified in the y_dist argument of maxlogLreg.

See also

Other maxlogL: cum_hazard.maxlogL(), maxlogLreg(), maxlogL()

Author

Jaime Mosquera Gutiérrez, jmosquerag@unal.edu.co

Examples

library(EstimationTools)

#----------------------------------------------------------------------------
# Example 1: mean value of a estimated model.
n <- 100
x <- runif(n = n, -5, 6)
y <- rnorm(n = n, mean = -2 + 3 * x, sd = 0.3)
norm_data <- data.frame(y = y, x = x)

formulas <- list(sd.fo = ~ 1, mean.fo = ~ x)
support <- list(interval = c(-Inf, Inf), type = "continuous")

norm_mod_maxlogL <- maxlogLreg(
  formulas, y_dist = y ~ dnorm,
  support = support,
  data = norm_data,
  link = list(over = "sd", fun = "log_link")
)

# Actual y values
y <- norm_mod_maxlogL$outputs$response

# Expected value
Ey <- expected_value.maxlogL(
  object = norm_mod_maxlogL,
  routine = "monte-carlo"
)

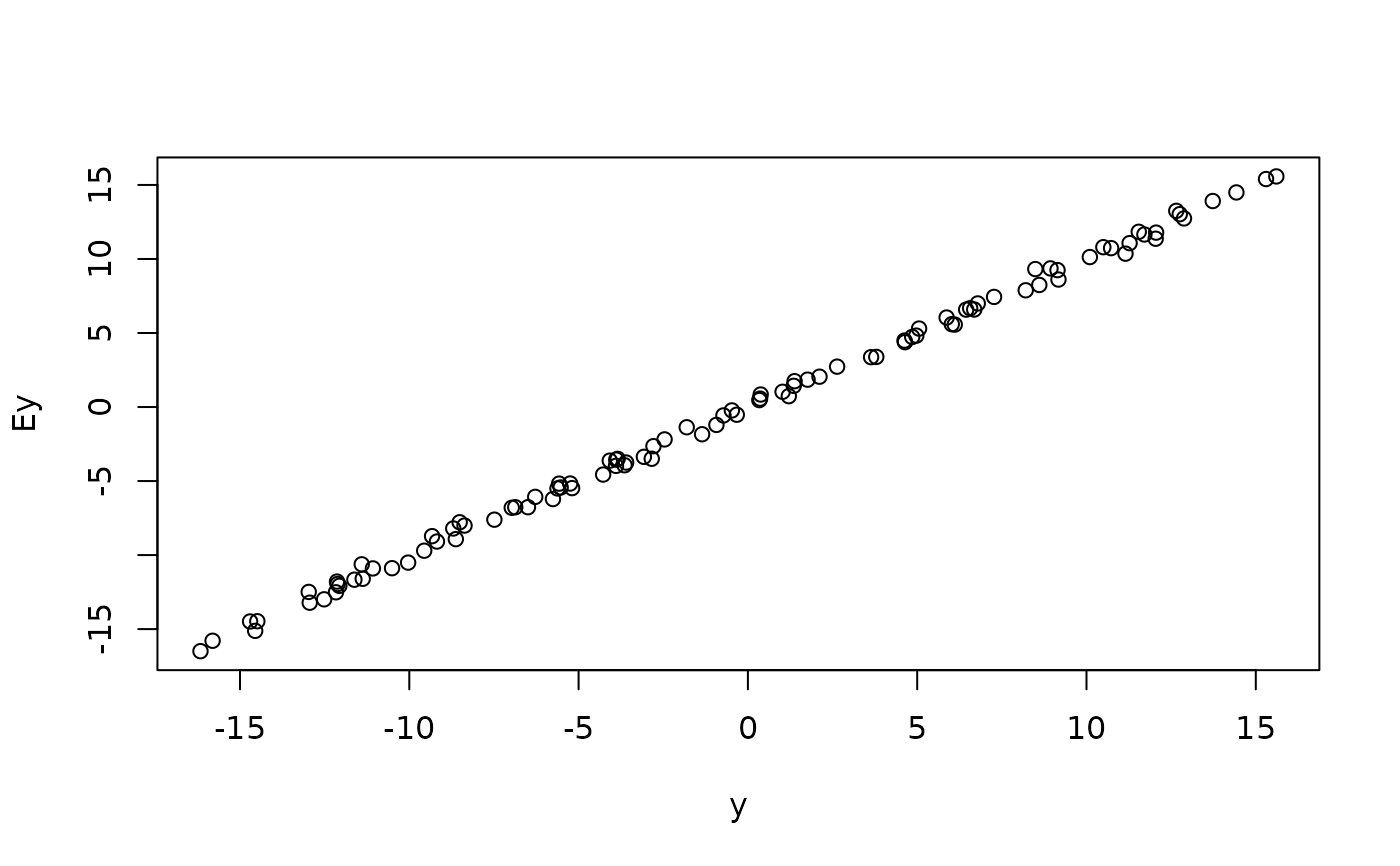
# Compare
plot(y, Ey)



#----------------------------------------------------------------------------